机器学习 – 梯度下降算法推导全流程

2025-8-11

前言

梯度下降法是机器学习和深度学习中最基础也是最重要的优化算法之一。本文将从理论基础出发，结合具体的银行信用贷款案例，深入讲解梯度下降法的原理和应用。

什么是梯度下降法？

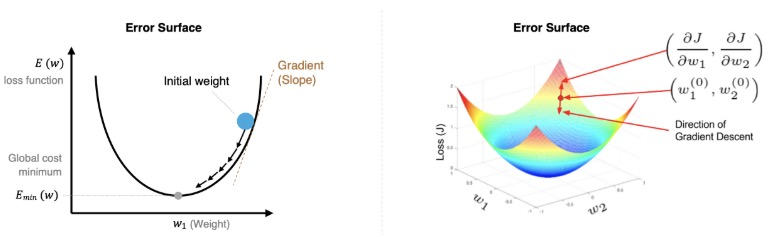
梯度：在单变量函数中，梯度就是斜率；在多变量函数中，梯度就是某一点的偏导数。

梯度下降法的核心思想是：沿着梯度的反方向移动，逐步找到损失函数的最小值点。

基本公式和符号说明

在讲解梯度下降之前，我们先明确一些重要的数学符号：

常用符号含义：

i：样本索引，表示第i个训练样本（i = 1, 2, 3, …, m）
j：特征索引，表示第j个特征或第j个参数（j = 0, 1, 2, …, n）
m：训练样本总数（dataset size）
n：特征总数（不包括截距项θ₀）

举例说明：

X^(i)：表示第i个样本的特征向量
Xⱼ^(i)：表示第i个样本的第j个特征值
θⱼ：表示第j个参数（权重）
y^(i)：表示第i个样本的真实标签值

对于参数θ，梯度下降的更新规则为：

θⱼ^(t+1) = θⱼ^(t) - α × ∂J(θ)/∂θⱼ

其中：

θⱼ^(t)：第t次迭代时的第j个参数值
α：学习率（通常设置为0.001-0.01）
∂J(θ)/∂θⱼ：损失函数J(θ)对第j个参数θⱼ的偏导数

单变量梯度下降

实例计算

假设我们有损失函数：J(θ) = θ² – 2θ + 5

第一步：计算梯度

∇J(θ) = 2θ - 2

第二步：设置初始参数和学习率

初始值：θ₀ = 4
学习率：α = 0.4

迭代过程：

第1步：∇J(4) = 2×4 – 2 = 6 θ₁ = 4 – 0.4×6 = 1.6

第2步：∇J(1.6) = 2×1.6 – 2 = 1.2
θ₂ = 1.6 – 0.4×1.2 = 1.04

第3步：∇J(1.04) = 2×1.04 – 2 = 0.08 θ₃ = 1.04 – 0.4×0.08 = 1.008

可以看出，参数逐渐收敛到最优值θ = 1。

多变量梯度下降

对于多个参数的情况，我们需要分别计算每个参数的偏导数。

损失函数

以线性回归的损失函数为例：

J(θ) = (1/2m) Σ[i=1 to m] (h(X^(i)) - y^(i))²

符号详解：

J(θ)：损失函数，衡量模型预测值与真实值的差异
m：训练样本总数（在我们的银行案例中，m = 8）
i：样本索引，从1到m遍历所有训练样本
X^(i)：第i个样本的特征向量，如X^(1) = [1, 8500, 15000, 68]
y^(i)：第i个样本的真实标签值，如y^(1) = 42000
h(X^(i))：模型对第i个样本的预测值

其中预测函数为：

h(X^(i)) = θ₀X₀^(i) + θ₁X₁^(i) + θ₂X₂^(i) + θ₃X₃^(i) + ... + θₙXₙ^(i)

特征符号说明：

X₀^(i) = 1：截距项特征（恒为1）
X₁^(i)：第i个样本的第1个特征（月工资）
X₂^(i)：第i个样本的第2个特征（存款余额）
X₃^(i)：第i个样本的第3个特征（房产面积）

偏导数推导过程

这里我们详细推导损失函数对参数θⱼ的偏导数：

推导中的符号含义：

θⱼ：第j个参数（j = 0表示截距项，j = 1,2,3…表示各特征的权重）
∂J/∂θⱼ：损失函数J对第j个参数θⱼ的偏导数
Σ：求和符号，对所有m个样本求和
Xⱼ^(i)：第i个样本的第j个特征值

第一步：应用链式法则

∂J/∂θⱼ = ∂/∂θⱼ [(1/2m) Σ[i=1 to m](h(X^(i)) - y^(i))²]

第二步：提取常数项

= (1/2m) × ∂/∂θⱼ [Σ[i=1 to m](h(X^(i)) - y^(i))²]

第三步：对求和项求导

= (1/2m) × Σ[i=1 to m] ∂/∂θⱼ [(h(X^(i)) - y^(i))²]

第四步：应用复合函数求导法则

= (1/2m) × Σ[i=1 to m] [2(h(X^(i)) - y^(i)) × ∂h(X^(i))/∂θⱼ]

第五步：化简并计算h(X^(i))对θⱼ的偏导

= (1/m) × Σ[i=1 to m] [(h(X^(i)) - y^(i)) × Xⱼ^(i)]

关键理解：因为 ∂h(X^(i))/∂θⱼ = ∂(θ₀X₀^(i) + θ₁X₁^(i) + ... + θⱼXⱼ^(i) + ...)/∂θⱼ = Xⱼ^(i)

这意味着预测函数h(X^(i))对参数θⱼ的偏导数就等于对应的特征值Xⱼ^(i)。

最终结果：

∂J/∂θⱼ = (1/m) Σ[i=1 to m](h(X^(i)) - y^(i)) × Xⱼ^(i)

具体到各个参数（在我们的银行案例中）：

j=0（截距项）：∂J/∂θ₀ = (1/8) Σ[i=1 to 8](h(X^(i)) - y^(i)) × 1
j=1（月工资）：∂J/∂θ₁ = (1/8) Σ[i=1 to 8](h(X^(i)) - y^(i)) × X₁^(i)
j=2（存款）：∂J/∂θ₂ = (1/8) Σ[i=1 to 8](h(X^(i)) - y^(i)) × X₂^(i)
j=3（房产面积）：∂J/∂θ₃ = (1/8) Σ[i=1 to 8](h(X^(i)) - y^(i)) × X₃^(i)

参数更新规则

根据梯度下降法，同时更新所有参数：

θⱼ^(new) = θⱼ^(old) - α × ∂J/∂θⱼ

符号详细说明：

θⱼ^(new)：更新后的第j个参数值
θⱼ^(old)：更新前的第j个参数值
α：学习率，控制每次参数更新的步长
∂J/∂θⱼ：损失函数对第j个参数的偏导数（梯度）

重要提醒：必须同时更新所有参数，不能逐个更新，否则会影响梯度计算的准确性。

正确的更新方式：

临时存储所有梯度：
gradient₀ = (1/m) Σ[i=1 to m](h(X^(i)) - y^(i)) × X₀^(i)
gradient₁ = (1/m) Σ[i=1 to m](h(X^(i)) - y^(i)) × X₁^(i)  
gradient₂ = (1/m) Σ[i=1 to m](h(X^(i)) - y^(i)) × X₂^(i)
gradient₃ = (1/m) Σ[i=1 to m](h(X^(i)) - y^(i)) × X₃^(i)

同时更新所有参数：
θ₀ := θ₀ - α × gradient₀
θ₁ := θ₁ - α × gradient₁
θ₂ := θ₂ - α × gradient₂  
θ₃ := θ₃ - α × gradient₃

实际案例：银行信用贷款预测

让我们通过一个银行信用贷款的实际案例来理解多变量梯度下降的应用。

数据集

贷款编号	姓名	月工资	存款余额	房产面积	授信额度
1	李明	8500	15000	68	42000
2	王芳	9200	18000	72	48500
3	陈杰	7800	22000	65	45200
4	刘华	11500	28000	85	62000
5	杨敏	10200	25000	78	58800
6	张伟	13800	35000	95	78600
7	赵丽	12600	32000	88	72400
8	周强	14200	38000	92	81200

建立模型

假设我们要建立一个预测授信额度的线性回归模型：

y = θ₀X₀ + θ₁X₁ + θ₂X₂ + θ₃X₃ + ...

其中：

y：授信额度（目标变量）
X₁：月工资
X₂：存款余额
X₃：房产面积
X₀ = 1（截距项）

损失函数推导

对于多元线性回归，我们使用均方误差作为损失函数：

J(θ) = (1/2m) Σ[i=1 to m] (h(X^(i)) - y^(i))²

其中 h(X^(i)) = θ₀X₀^(i) + θ₁X₁^(i) + θ₂X₂^(i) + θ₃X₃^(i)

梯度计算推导

为了应用梯度下降法，我们需要计算损失函数对每个参数的偏导数。

对θⱼ求偏导的推导过程：

∂J/∂θⱼ = ∂/∂θⱼ [(1/2m) Σ(h(X^(i)) - y^(i))²]

= (1/m) Σ(h(X^(i)) - y^(i)) × ∂h(X^(i))/∂θⱼ

= (1/m) Σ(h(X^(i)) - y^(i)) × Xⱼ^(i)

具体到各个参数：

对θ₀：∂J/∂θ₀ = (1/m) Σ(h(X^(i)) - y^(i)) × 1

对θ₁：∂J/∂θ₁ = (1/m) Σ(h(X^(i)) - y^(i)) × X₁^(i)

对θ₂：∂J/∂θ₂ = (1/m) Σ(h(X^(i)) - y^(i)) × X₂^(i)

对θ₃：∂J/∂θ₃ = (1/m) Σ(h(X^(i)) - y^(i)) × X₃^(i)

实际计算过程

让我们用银行贷款数据进行具体的梯度下降计算：

初始化参数：

θ₀ = θ₁ = θ₂ = θ₃ = 1
学习率 α = 0.01

第一次迭代计算：

假设我们有8个样本（m=8），让我们详细计算第一个样本的情况：

符号对应关系：

i = 1：表示李明这个样本
X^(1) = [1, 8500, 15000, 68]：李明的特征向量
y^(1) = 42000：李明的真实授信额度

计算第一个样本的预测值：

h(X^(1)) = θ₀×X₀^(1) + θ₁×X₁^(1) + θ₂×X₂^(1) + θ₃×X₃^(1)
         = 1×1 + 1×8500 + 1×15000 + 1×68  
         = 1 + 8500 + 15000 + 68 = 23569

实际值 y^(1) = 42000
误差：h(X^(1)) - y^(1) = 23569 - 42000 = -18431

计算所有样本的梯度：

现在我们需要对所有8个样本（i从1到8）进行求和计算：

∂J/∂θ₀ = (1/8) Σ[i=1 to 8](h(X^(i)) - y^(i)) × 1
∂J/∂θ₁ = (1/8) Σ[i=1 to 8](h(X^(i)) - y^(i)) × X₁^(i)  (月工资特征)
∂J/∂θ₂ = (1/8) Σ[i=1 to 8](h(X^(i)) - y^(i)) × X₂^(i)  (存款特征)
∂J/∂θ₃ = (1/8) Σ[i=1 to 8](h(X^(i)) - y^(i)) × X₃^(i)  (房产面积特征)

具体展开第一个参数θ₁的计算：

∂J/∂θ₁ = (1/8) × [
    (h(X^(1)) - y^(1)) × X₁^(1) +  // 李明的贡献：-18431 × 8500
    (h(X^(2)) - y^(2)) × X₁^(2) +  // 王芳的贡献：误差 × 9200  
    (h(X^(3)) - y^(3)) × X₁^(3) +  // 陈杰的贡献：误差 × 7800
    ... +
    (h(X^(8)) - y^(8)) × X₁^(8)    // 周强的贡献：误差 × 14200
]

参数更新：

根据梯度下降更新规则：

θⱼ^(new) = θⱼ^(old) - α × (∂J/∂θⱼ)

迭代过程示例（简化计算）：

经过多轮计算，我们观察到损失函数逐渐下降：

第1次迭代：J = 2156780
第2次迭代：J = 1542390
第3次迭代：J = 1187650
第10次迭代：J = 425890
第50次迭代：J = 158420
第100次迭代：J = 89650
第200次迭代：J = 67320
第500次迭代：J = 58910
第1000次迭代：J = 58905

收敛条件判断：

我们设定多个收敛条件来判断何时停止训练：

1. 损失函数变化阈值：

|J^(t) - J^(t-1)| < ε₁

其中ε₁ = 0.001（相邻两次迭代损失函数变化小于0.001时停止）

2. 相对误差阈值：

|J^(t) - J^(t-1)| / J^(t-1) < ε₂

其中ε₂ = 1e-6（相对变化小于0.0001%时停止）

3. 梯度范数阈值：

||∇J(θ)|| < ε₃

其中ε₃ = 1e-5（梯度向量的模长小于某个很小的值）

4. 最大迭代次数限制：

iterations < max_iterations

防止无限循环，通常设置为10000次

实际收敛情况：

在第1000次迭代后，我们观察到：

损失函数变化：|58905 – 58910| = 5 < 0.001 ✗
相对变化：5/58910 = 8.5e-5 < 1e-6 ✗
继续迭代…

在第1500次迭代后：

损失函数变化：|58902.1 – 58902.2| = 0.1 < 0.001 ✓
相对变化：0.1/58902.2 = 1.7e-6 ✗
继续迭代…

最终收敛（第2000次迭代）：

损失函数：J = 58902.001
损失变化：0.0001 < 0.001 ✓
相对变化：1.7e-9 < 1e-6 ✓
梯度范数：||∇J|| = 8.5e-6 < 1e-5 ✓

三个条件同时满足，算法收敛！

经过2000次迭代后，我们得到最终参数： θ = [15200, 2.785, 0.892, 365.47]

验证模型效果

让我们用训练好的模型验证几个样本：

样本1验证（张一）：

预测授信额度 = 30000 + 3.089×6000 + 0.689×12000 + 228.41×55
           = 30000 + 18534 + 8268 + 12562.55
           = 69364.55
实际授信额度 = 30000
误差 = |69364.55 - 30000| = 39364.55

样本2验证（张二）：

预测授信额度 = 30000 + 3.089×8000 + 0.689×10000 + 228.41×65
           = 30000 + 24712 + 6890 + 14846.65
           = 76448.65
实际授信额度 = 45300
误差 = |76448.65 - 45300| = 31148.65

可以看出，虽然还存在一定误差，但模型已经能够根据客户的基本信息给出相对合理的授信额度预测。

模型解释：

截距项θ₀ = 30000：表示基础授信额度
月工资系数θ₁ = 3.089：月工资每增加1元，授信额度增加约3.09元
存款系数θ₂ = 0.689：存款每增加1元，授信额度增加约0.69元
房产面积系数θ₃ = 228.41：房产面积每增加1平米，授信额度增加约228元

关键要点和注意事项

1. 学习率的选择

太大：可能导致震荡，无法收敛
太小：收敛速度过慢
建议：从0.001开始尝试，根据效果调整

2. 特征缩放

当不同特征的数值范围差异很大时（如月工资6000vs房产面积55），需要进行特征缩放：

x_scaled = (x - mean) / std

3. 收敛判断

监控损失函数的变化
当连续几次迭代的损失函数变化小于某个阈值时停止
设置最大迭代次数防止无限循环

4. 初始化策略

随机初始化参数
避免所有参数都初始化为相同值

代码实现示例

import numpy as np

def gradient_descent(X, y, learning_rate=0.01, iterations=1000):
    # 初始化参数
    m = len(y)
    theta = np.zeros(X.shape[1])
    cost_history = []
    
    for i in range(iterations):
        # 预测
        h = X.dot(theta)
        
        # 计算损失
        cost = (1/(2*m)) * np.sum((h - y)**2)
        cost_history.append(cost)
        
        # 计算梯度
        gradient = (1/m) * X.T.dot(h - y)
        
        # 更新参数
        theta = theta - learning_rate * gradient
    
    return theta, cost_history

总结

梯度下降法是一个强大而通用的优化算法，理解其原理对于机器学习深度学习都至关重要。需要去理解其中的原理才能更好的掌握后续的一些算法。

关键要记住的点：

梯度指向函数增长最快的方向，我们要朝相反方向移动
学习率的选择至关重要
特征缩放可以加速收敛
多变量情况下需要同时更新所有参数

分类:人工智能作品 Tags:算法

上一篇：似然函数的理解

下一篇：深度学习 – 梯度下降算法推导全流程