前言
上次把机器学习的梯度下降算法公式推导了一遍,但是在神经网络里,梯度下降算法还做了很多优化,本文目标从深度学习这个方向解析梯度下降的工作机制、前向反向传播的计算过程,以及各种优化策略,揭开深度学习梯度下降算法的面纱。
一、梯度下降算法概述
算法目的
梯度下降算法的目的是优化网络,让预测值和真实值的差异越来越小,也就是损失函数越小越好。
数学原理
梯度下降算法是一种寻找使得损失函数最小化的方法。从数学角度上,梯度的方向就是函数增长速度最快的方向,那么梯度的反方向就是函数减少最快的方向。
参数更新公式:
Wⱼ^(new) = Wⱼ^(old) - α × ∂J/∂Wⱼ
为什么选择梯度下降?
让损失函数最小化有两种方法:
- 直接求导数为0:在深度学习中,网络规模大,参数众多,求导直接为0不太好做,而且很可能解决不了,这个过程中有矩阵的逆之类的处理。
- 梯度下降算法:所以深度学习找最优解,只有梯度下降算法。
学习率α的设置
学习率α的设置不能太大,也不能太小:
- 太小:训练的时间会增加
- 太大:可能直接跳过最优解,进入到无限的训练中
解决办法就是学习率也需要随着训练的进行而变化。
二、批量训练策略
在进行模型训练时,有三个基础概念:
- Epoch: 使用全部数据对模型进行一次完整训练,训练轮次
- Batch_size: 使用训练集中的小部分样本对模型权重进行一次反向传播的参数更新,每次训练每批次样本数量
- Iteration: 迭代次数,使用一个 Batch 数据对模型进行一次参数更新的过程
三种梯度下降算法对比
假设有5万个样本,不同的训练策略如下:
| 梯度下降算法 | 训练集 | Batch Size | Number of Batch | 备注 |
|---|---|---|---|---|
| BGD(全梯度) | N | N | 1 | 深度学习中不现实,因为数据量很大 |
| SGD(随机梯度) | N | 1 | N | 也不现实,因为异常值对结果影响很大,造成很大的波 动 |
| Mini-Batch(小批量梯度) | N | B | N/B+1 | B是越大越好,但是取决于硬件 |
- Mini-Batch中的Batch个数,N/B+1是针对未整除的情况,如果整除的话是N/B
- 但是Mini-Batch在代码中通常叫SGD
三、深度学习网络结构
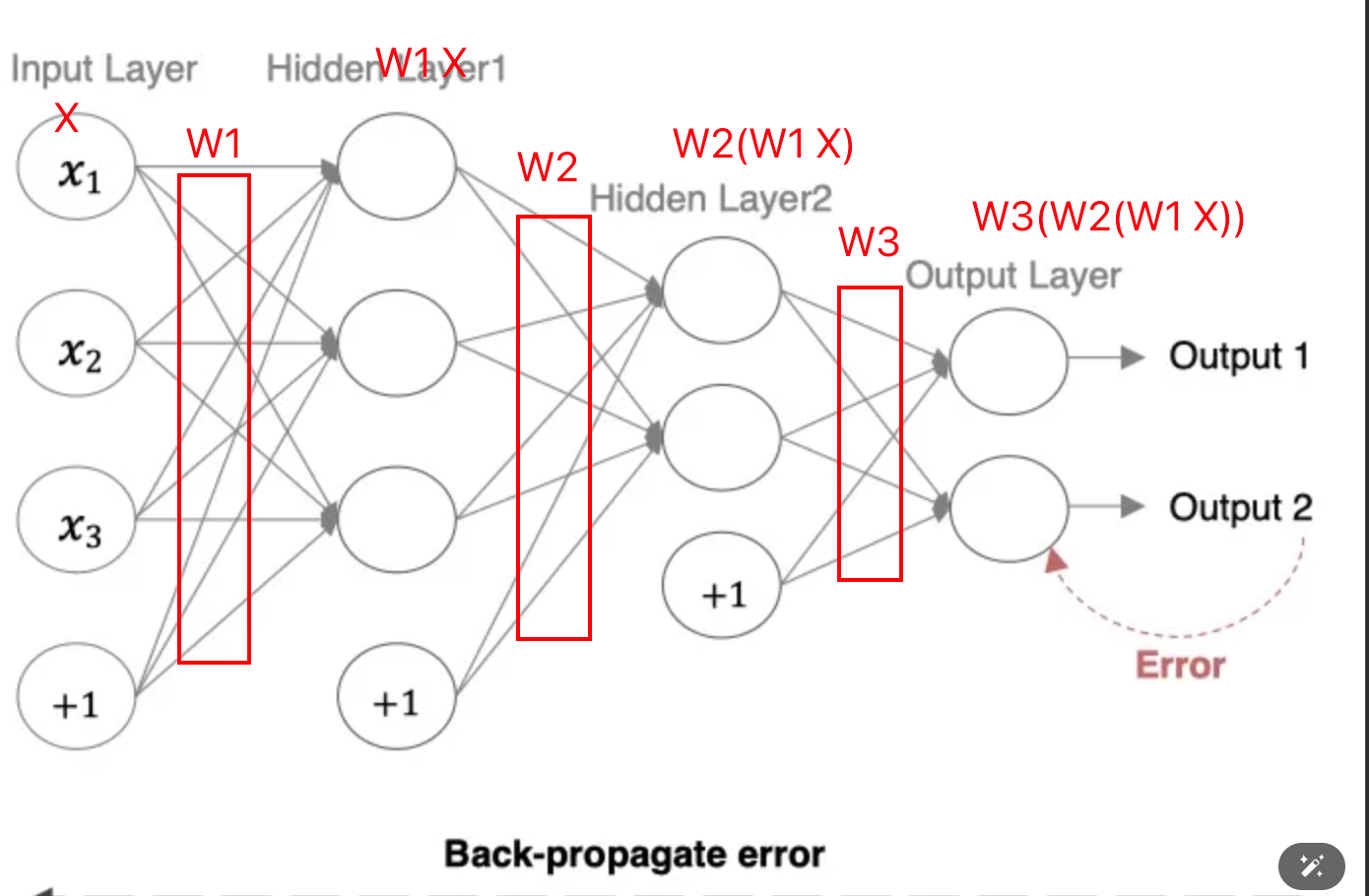
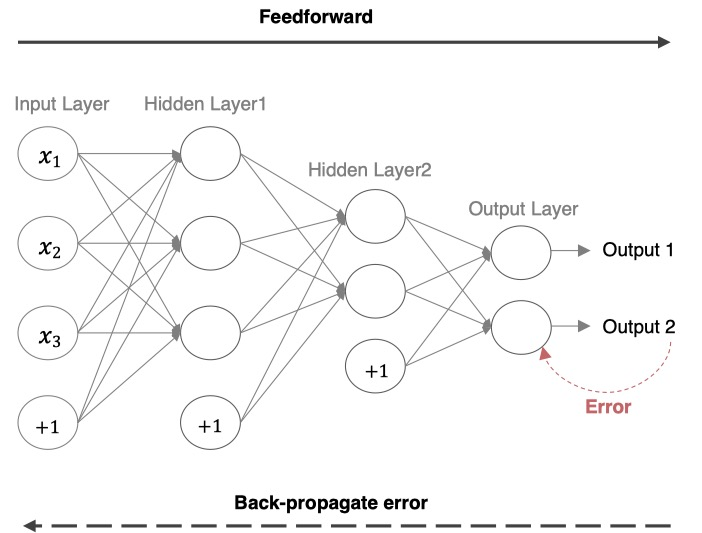
深度学习网络的基本流程包括:
- 前向传播:获取预测结果
- 计算损失loss:预测结果与真实结果的差异,使用交叉熵或MSE
- 反向传播:参数更新
最后output得到的数据是W3(W2(W1 × X))与真实值的差距,所以要从W3(W2(W1 × X))来计算。根据复合函数求导,先对W3求导,更新完W3,再去更新W2,最后W1。所以更新过程是从右(输出层)到左(输入层)的,也叫backward。
四、前向传播详细计算
概念:把输入送给网络进行预测的过程我们称之为前向传播。
神经网络的计算流程示例
以一个具体的三层神经网络为例:
输入参数设置:
- 输入:i1 = 0.05, i2 = 0.10
- 权重:w1 = 0.15, w2 = 0.20, w3 = 0.25, w4 = 0.3
- 权重:w5 = 0.4, w6 = 0.45, w7 = 0.50, w8 = 0.55
- 偏置:b1 = 0.35, b2 = 0.60
- 目标值:target1 = 0.01, target2 = 0.01
1. 隐藏层计算
净输入计算:
net_h1 = w1 × i1 + w2 × i2 + b1 = 0.15 × 0.05 + 0.20 × 0.10 + 0.35 × 1 = 0.3775 net_h2 = w3 × i1 + w4 × i2 + b1 = 0.25 × 0.05 + 0.3 × 0.1 + 0.35 × 1 = 0.3925
激活函数输出(使用Sigmoid):
out_h1 = 1/(1+e^(-net_h1)) = 1/(1+e^(-0.3775)) = 0.593269992 out_h2 = 1/(1+e^(-net_h2)) = 1/(1+e^(-0.3925)) = 0.596884378
2. 输出层的计算
这里隐藏层的激活函数是sigmoid,为了方便计算输出层的激活函数也是sigmoid,实际使用应该是softmax。
净输入计算:
net_o1 = w5 × out_h1 + w6 × out_h2 + b2 = 0.4 × 0.593269992 + 0.45 × 0.596884378 + 0.60 = 1.105905967
net_o2 = w7 × out_h1 + w8 × out_h2 + b2 = 0.50 × 0.593269992 + 0.55 × 0.596884378 + 0.6 = 1.224
最终输出:
out_o1 = 1/(1+e^(-net_o1)) = 1/(1+e^(-1.105905967)) = 0.75136507
out_o2 = 1/(1+e^(-net_o2)) = 0.772928465
3. 总误差的计算
为了计算方便,这里的loss计算使用的是MSE,实际应用中通常选择交叉熵。
out_o1的MSE:
E_o1 = Σ(1/num × (target - output)²) = 0.274811083
其中:target = 0.01,output = 0.75136507,num = 2(样本个数)
out_o2的MSE:
E_o2 = Σ(1/num × (target - output)²) = 0.023560026
其中:target = 0.01,output = 0.772928465,num = 2
总误差:
E_total = E_o1 + E_o2 = 0.274811083 + 0.023560026 = 0.298371109
五、反向传播详细推导

概念:利用损失函数loss,从后往前,结合梯度下降算法,依次求各个参数的偏导,并进行参数更新的过程称之为反向传播。
输出层参数更新
从输出层往隐藏层更新参数。更新参数需要用老的权重减去新的权重,新的权重通过求导数获得。
更新顺序:先对输出层的o1、o2更新,再对隐藏层的h1、h2更新。o1对应w5、w6,o2对应w7、w8,h1对应w1、w2,h2对应w3、w4。
简化版本的损失函数:
loss_o1 = (sigmoid(out_h1 × w5 + out_h2 × w6 + b2) - target)^2
对w5求导时,需要从外层到里层一点点展开复合函数求导:
- 先对平方求导,再对里面out_o1求导,再对net_o1求导,再对w5求导
- 从外层到内层依次求导
具体推导过程:计算总误差对权重w5的偏导
核心链式关系:
∂E_total/∂w5 = (∂E_total/∂out_o1) × (∂out_o1/∂net_o1) × (∂net_o1/∂w5)
1. 误差定义
单输出o1误差:
E_o1 = 1/2 × (target_o1 - out_o1)²
总误差:
E_total = E_o1 + E_o2
完整总误差展开:
E_total = 1/2 × (target_o1 - out_o1)² + 1/2 × (target_o2 - out_o2)²
2. 总误差对out_o1的偏导
对E_total关于out_o1求导(仅E_o1含out_o1,E_o2的导数自然为0):
∂E_total/∂out_o1 = ∂E_o1/∂out_o1 = -(target_o1 - out_o1) = out_o1 - target_o1
代入数值(假设target_o1 = 0.01,out_o1 = 0.75136507):
∂E_total/∂out_o1 = 0.75136507 - 0.01 = 0.74136507
3. 输出out_o1对净输入net_o1的偏导
out_o1是Sigmoid激活函数:
out_o1 = 1/(1 + e^(-net_o1))
其导数性质为:
∂out_o1/∂net_o1 = out_o1 × (1 - out_o1)
代入数值(out_o1 = 0.75136507):
∂out_o1/∂net_o1 = 0.75136507 × (1 - 0.75136507) = 0.186815602
4. 净输入net_o1对权重w5的偏导
net_o1定义:
net_o1 = w5 × out_h1 + w6 × out_h2 + b2
对w5求导:
∂net_o1/∂w5 = out_h1
代入数值:
∂net_o1/∂w5 = out_h1 = 0.593269992
5. 总误差对w5的偏导(链式法则乘积)
根据链式法则,总误差对w5的偏导为三步偏导的乘积:
∂E_total/∂w5 = (∂E_total/∂out_o1) × (∂out_o1/∂net_o1) × (∂net_o1/∂w5)
代入数值计算:
∂E_total/∂w5 = 0.74136507 × 0.186815602 × 0.593269992 = 0.082167041
然后依次对所有的w6、w7、w8、w1、w2、w3、w4、b1、b2等参数进行求导更新。
隐藏层参数更新
隐藏层跟输出层的区别:w5只需要考虑o1就可以,但是更新w1时,它会影响o1和o2,所以o1和o2的损失都得对w1进行求导,针对求导的结果再去更新w1。
1. 总误差对w1的链式求导
∂E_total/∂w1 = (∂E_total/∂out_h1) × (∂out_h1/∂net_h1) × (∂net_h1/∂w1)
其中:
∂E_total/∂out_h1:总误差对隐藏层输出out_h1的偏导,需考虑out_h1对o1、o2的影响∂out_h1/∂net_h1:隐藏层激活函数(Sigmoid)的导数∂net_h1/∂w1:隐藏层净输入对w1的偏导
2. 总误差对隐藏层输出的分解
总误差由E_o1和E_o2组成(E_total = E_o1 + E_o2),因此:
∂E_total/∂out_h1 = ∂E_o1/∂out_h1 + ∂E_o2/∂out_h1
需要分别计算out_h1对o1和o2的影响。
3. 梯度计算的完整链式展开
∂E_total/∂w1 = [(∂E_o1/∂out_o1) × (∂out_o1/∂net_o1) × (∂net_o1/∂out_h1) +
(∂E_o2/∂out_o2) × (∂out_o2/∂net_o2) × (∂net_o2/∂out_h1)] ×
(∂out_h1/∂net_h1) × (∂net_h1/∂w1)
4. w1的更新(梯度下降)
学习率α = 0.5时,参数更新公式:
w1^(new) = w1^(old) - α × ∂E_total/∂w1
代入数值(根据完整计算):
w1^(new) = 0.15 - 0.5 × 0.000438568 = 0.149780716
六、梯度下降算法的优化方法
面临的问题
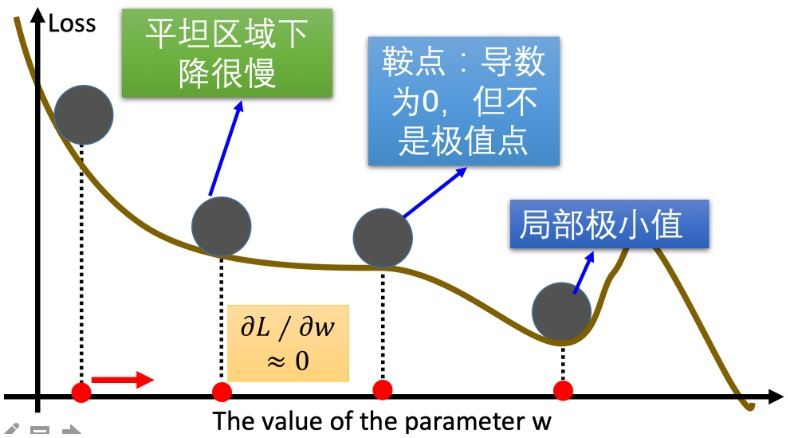
在实际应用中,标准梯度下降算法面临几个主要问题:
问题1:计算梯度时损失曲线有波动,平坦区域(导数比较小)影响了更新速度,我们希望在平坦区域更新得快一点,缩短训练时间。
问题2:鞍点问题,导数为0,但不是极值点。
问题3:局部最小值,没有更好的办法。但也有优势:在训练集表现好时发生过拟合,可能具备好的泛化能力。
改进方法
针对第一个和第二个问题,有以下改进方法:
- Momentum(重点)
- AdaGrad
- RMSprop
- Adam(重点)
对当前计算出来的梯度进行指数加权平均,可以使梯度曲线平缓很多。
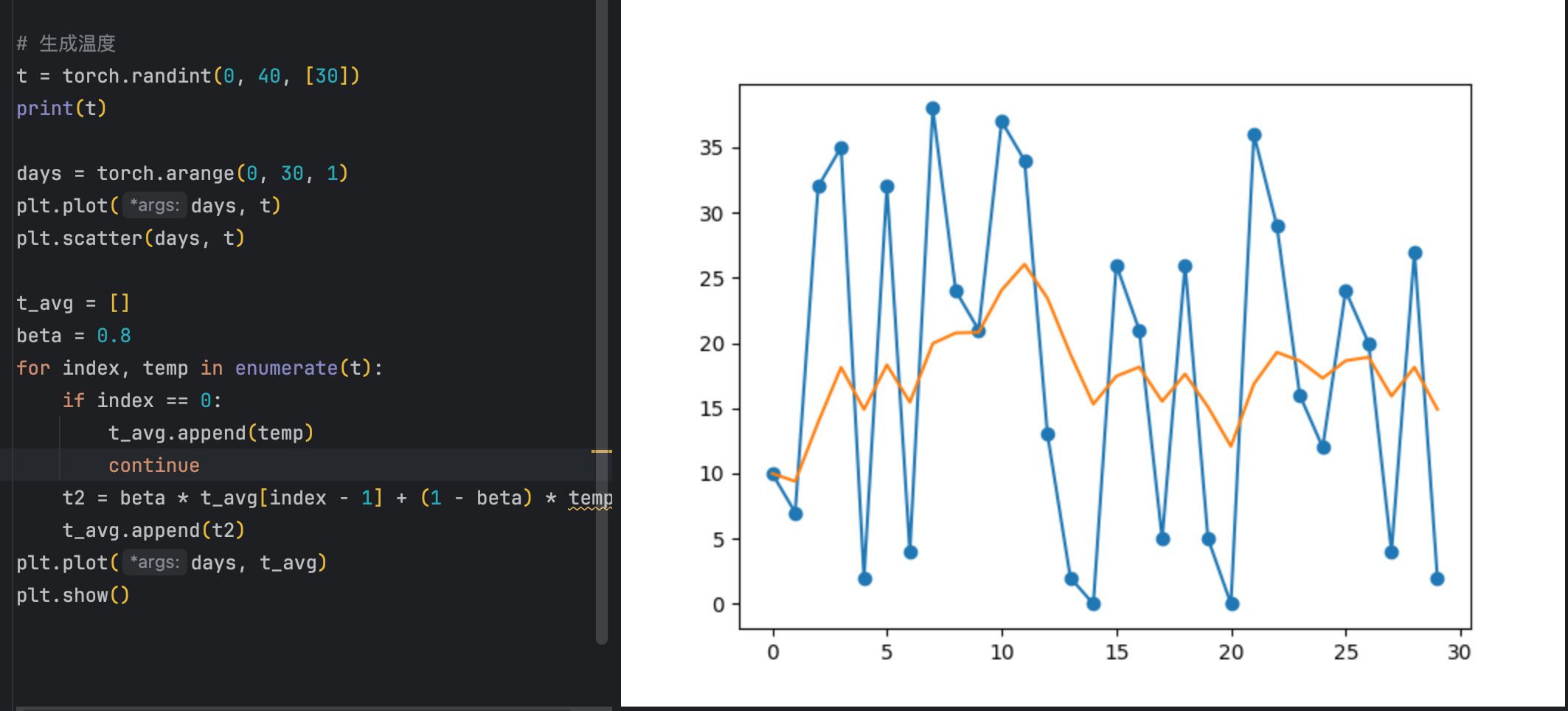
指数加权平均
公式:
St = β × St-1 + (1-β) × Yt
其中:
- St表示:指数加权平均值
- Yt表示:t时刻的值
- β:调节权重系数,该值越大平均数越平缓
Momentum动量法
更新公式:
Wⱼ^(new) = Wⱼ^(old) - α × Dt
Dt = β × St-1 + (1-β) × Wt
为了改进上面的两个问题,Dt不能是当前梯度,而是除了当前次迭代梯度外,以前迭代各次梯度的指数加权平均。
其中:
- Wt:表示当前次迭代的梯度
- St-1:表示历史梯度移动加权平均值
- Dt:为当前时刻的指数加权平均梯度值
- β:调节权重系数
解决的问题:
- 鞍点问题:当遇到鞍点时前面的梯度肯定不是0,正常鞍点无法更新梯度,我们可以通过这个新的平均梯度值,避免鞍点的问题。
- 平缓区域加速:如果当前区域比较平缓,本身的梯度比较小,但是前面比较大,所以会影响到Dt的结果,会让这个梯度变大,加快训练的进程。
- 减少震荡:如果mini-batch选取的样本比较小时,选取异常值,梯度可能跟前面的差异很大,通过momentum可以缓解这种震荡。
PyTorch代码示例:
标准SGD:
import torch
import numpy as np
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
loss = ((w ** 2) * 0.5).sum()
optim = torch.optim.SGD([w], lr=0.01)
optim.zero_grad()
loss.backward()
optim.step()
print(f'梯度:{w.grad}') # tensor([1.])
print(f'权重:{w.detach()}') # tensor([0.9900])
# 第二次更新
loss = ((w ** 2) * 0.5).sum()
optim.zero_grad()
loss.backward()
optim.step()
print(f'更新后梯度:{w.grad}') # tensor([0.9900])
print(f'更新后权重:{w.detach()}') # tensor([0.9801])
带动量的SGD:
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
loss = ((w ** 2) * 0.5).sum()
optim = torch.optim.SGD([w], lr=0.01, momentum=0.9)
optim.zero_grad()
loss.backward()
optim.step()
print(f'梯度:{w.grad}')
print(f'权重:{w.detach()}')
print("***" * 20)
loss = ((w ** 2) * 0.5).sum()
optim.zero_grad()
loss.backward()
optim.step()
print(f'更新后梯度:{w.grad}')
print(f'更新后权重:{w.detach()}')
可以看到,加了momentum以后,因为受到之前的影响,更新速度会快一点。
AdaGrad法
原理:通过对不同的参数分量使用不同的学习率,这个参数分量是指不同的weight,就是整个神经网络里不同的weight使用不同的学习率,总体学习率随着迭代次数增加是在减少。
计算步骤:
- 初始化学习率α、初始化参数θ、小常数ε = 1e-7
- 初始化梯度累积变量r = 0
- 从训练集中采样m个样本的小批量,计算梯度g
- 累积平方梯度:r = r + g ⊙ g,⊙表示各个分量相乘
因为r这个值太大,导致学习率很小,所以对它进行开根号。
学习率α的计算公式:
α' = α / (√r + ε)
参数更新公式:
θ = θ - α' ⊙ g
重复2-4步骤,即可完成网络训练。
AdaGrad缺点:可能会使得学习率过早衰减,因为开方以后√r还是下降比较快的,学习率过量降低,导致模型训练后期学习率太小,较难找到最优解。
PyTorch代码示例:
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
loss = ((w ** 2) * 0.5).sum()
optim = torch.optim.Adagrad([w], lr=0.01)
optim.zero_grad()
loss.backward()
optim.step()
print(f'梯度:{w.grad}')
print(f'权重:{w.detach()}')
# 第二次更新
loss = ((w ** 2) * 0.5).sum()
optim.zero_grad()
loss.backward()
optim.step()
print(f'更新后梯度:{w.grad}')
print(f'更新后权重:{w.detach()}')
RMSprop方法
RMSprop优化算法是对AdaGrad的优化,最主要的不同是,其使用指数移动加权平均梯度替换历史梯度的平方和。
计算步骤:
- 初始化学习率α、初始化参数θ、小常数ε = 1e-7
- 初始化梯度累积变量r = 0
- 从训练集中采样m个样本的小批量,计算梯度g
- 累积平方梯度:s = β × s + (1-β) × g × g
参数更新公式:
θ = θ - α/(√s + ε) × g
因为s变小了,变相地减少学习率衰减的步伐。
PyTorch代码示例:
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
loss = ((w ** 2) * 0.5).sum()
# 这里的alpha对应的是beta
optim = torch.optim.RMSprop([w], lr=0.01, alpha=0.09)
# 第一次更新计算梯度,并且对参数进行更新
optim.zero_grad()
loss.backward()
optim.step()
print(f'梯度:{w.grad}')
print(f'权重:{w.detach()}')
# 第二次更新计算梯度,并且对参数进行更新
loss = ((w ** 2) * 0.5).sum()
optim.zero_grad()
loss.backward()
optim.step()
print(f'更新后梯度:{w.grad}')
print(f'更新后权重:{w.detach()}')
七、学习率衰减方法
学习率衰减一般跟Momentum一起组合使用,也可以跟其他的优化器组合。
等间隔衰减
随着学习轮次的增加,学习率越来越小,并且等间隔地进行学习率衰减。
设计这样的API,只需要设置间隔和衰减比例就可以了:
- 间隔是多少
- 衰减比例是多少
实现代码:
# 参数的初始化
lr0 = 0.1
iter = 100
epoches = 200
# 网络数据初始化
x = torch.tensor([1.0])
w = torch.tensor([1.0], requires_grad=True)
y = torch.tensor([1.0])
# 优化器构建
optimizer = torch.optim.SGD([w], lr=lr0, momentum=0.9)
# 学习率策略
lr_scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=20, gamma=0.5)
epoch_list = []
lr_list = []
# 遍历轮次
for epoch in range(epoches):
lr_list.append(lr_scheduler.get_last_lr())
epoch_list.append(epoch)
# 遍历batch
for i in range(iter):
pass
# 计算损失
loss = ((w * x - y) ** 2) * 0.5
# 更新参数
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 更新Lr
lr_scheduler.step()
# 绘制结果
plt.plot(epoch_list, lr_list)
plt.grid()
plt.show()
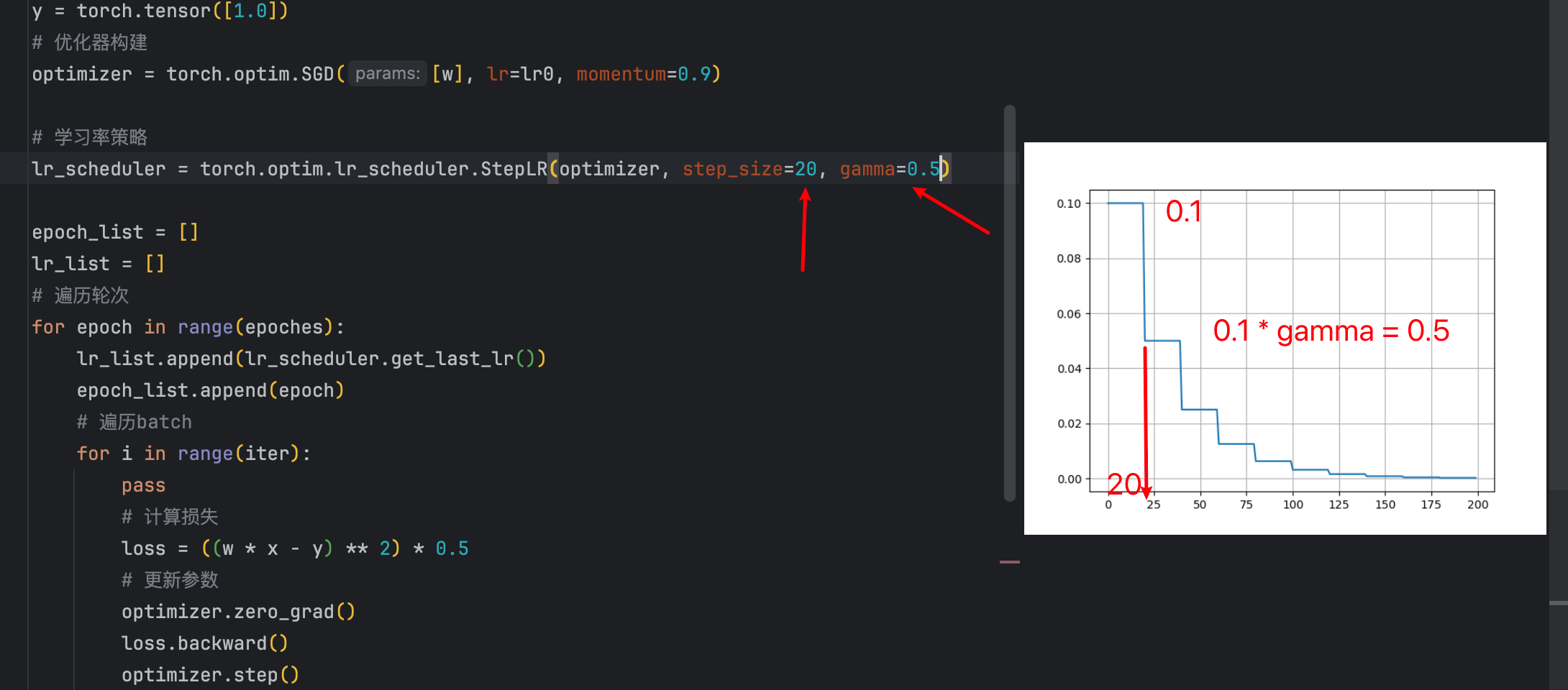
代码里每隔20次衰减一次,每次都是上一次的值乘以gamma也就是0.5。
等间隔衰减参数
- step_size:间隔多大
- gamma:衰减多少(是比例)
lr_scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=20, gamma=0.5)
指定间隔衰减参数
- milestones:指定在哪些epoch进行衰减
- gamma:衰减多少(是比例)
lr_scheduler = torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[50, 100, 200], gamma=0.5)
指数级别衰减
调整方式:lr = lr × gamma^epoch
就是gamma的轮次的指数次幂。gamma必须设置小于1,幂越高,gamma^epoch越小,所以lr越小。
所以lr是一直衰减的。
代码示例:
# 其他初始化代码相同... # 学习率策略 lr_scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.95) # 训练循环相同...
八、总结与展望
本文中我从问题分析到优化策略,从基础理论到实际应用的完整走了一遍;除此之外我们还需要注意一些注意事项的点。
核心要点回顾
- 数学基础的重要性:理解梯度、链式法则等数学概念是掌握算法精髓的基础
- 批量策略的权衡:Mini-Batch在计算效率和训练稳定性之间找到了最佳平衡
- 优化算法的演进:从SGD到Momentum再到Adam,每一步改进都针对具体问题
- 学习率调度的艺术:合适的学习率衰减策略能显著提升训练效果
实践建议
- 算法选择:对于大多数场景,SGD + Momentum + 学习率衰减是稳妥的选择
- 参数调优:从学习率开始调参,再逐步优化其他超参数
- 监控训练:通过损失曲线和梯度变化监控训练状态
- 持续学习:优化算法仍在快速发展,保持对新技术的关注
 沪ICP备2025124802号-1
沪ICP备2025124802号-1